Main Menu
| Noise and coupling enhance ordering |
|
Noise and coupling enhance ordering, synchronization, and resonance phenomena in
Physics and Biology
Collective behavior due to cooperative phenomena, leading to
synchronization as opposite to incoherence, plays an important role in
physical, biological, chemical, and social systems. In particular, these
facts have been observed in diverse fields of Science, such as
superconducting Josephson junctions arrays (SQUID).
Background A successful approach to the problem of synchronization consists of modeling each member of the population as a phase oscillator. Among the various phase models proposed to investigate the phenomena, the Kuramoto model appears as simple enough to be mathematically tractable, yet sufficiently complex to be nontrivial. The model is rich enough to display a large variety of synchronization patterns and sufficiently flexible to be adapted to many different contexts. Indeed, we have investigated deeply over the years the role played by the noise and coupling in the dynamics of oscillators. The noise appears here so as to account for unavoidable imperfections of various natures, and therefore it should be taken into account in any realistic description of the phenomena. In papers detailed below, we have reviewed extensively the progress made in the analysis of the model and its extensions during the last twenty-eight years. We have also tried to cover the most significant areas where the model has been applied so far.
The role played by noise and coupling on SQUIDs
The research on nonlinear oscillators has been focused in recent years on the field of Josephson junctions arrays, in part because of their numerous important technological applications, e.g., high operation frequencies and voltage standards, and because it consists in a very powerful and sensitive magnetometer. More specifically, we investigated a system of globally coupled two dimensional nonlinear oscillators, using the two-junction superconducting quantum interference device dc SQUID as a prototype for a single element. The dc SQUID has recently received considerable attention, since it is a device that is severely constrained by noise-floor issues and one in which a detailed study of the noise-mediated cooperative behavior in various regimes of operation can yield clever techniques for confronting noise-related performance issues that constrain current devices. We have investigated the dynamics of an array of globally coupled SQUIDs, and found that the coupling can lead to interesting effects. Indeed, the running frequency of the oscillatory solutions depends on the coupling, with large coupling and/or large number og SQUIDs reducing the frequency. This finding is extremely important, since coupling a time-sinusoidal target or probe signal to each SQUID leads to a resonance in the averaged screening current when the signal frequency approaches the running frequency. Thi resonance phenomenon affords the possibility of using a single device or an array as a power frequency sensitive detector.
Resonance phenomena in complex heterogeneous networks Other important parameter playing an important role in cooperative phenomena is the coupling among the various elements. In recent years, more realistic networks connecting the oscillators have been investigated, such as the scale-free interconnection network. This network of heteregoneous type models important complex phenomena in Nature, and many of its topological features has been characterized over the last years. However, a careful analysis of the dynamical properties was lacking.
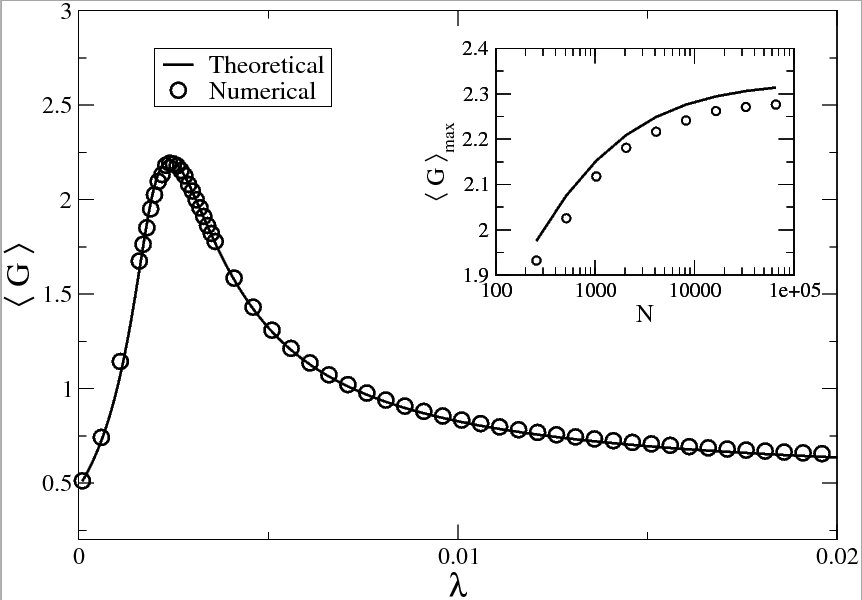
A sketchy diagram of a scale-free network Recently, we have investigated such properties focusing in the dynamics of signaling devices. These devices are the building blocks of many natural and artificial information-processing systems, and their proper functioning always require high sensitivity to external signals. We showed that an amplification of the external signal can be obtained in a deterministic dynamical system of signaling devices in complex heterogeneous networks. This is a remarkable finding, because usually this can be only be observed in presence of more complicated dynamics affected by noise. Moreover, it resembles some kind of topological resonance-like effect, and could explain the ubiquity of scale-free topological structure in Nature, more specifically in biological systems.
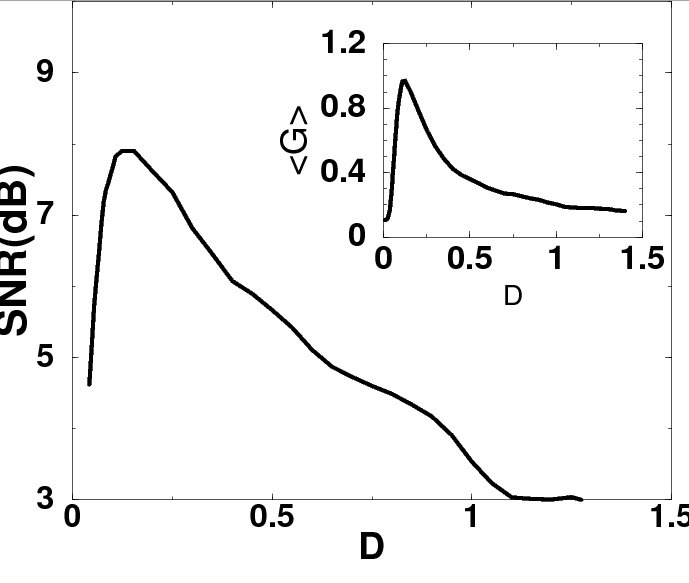
Amplification of the signal versus the coupling strength in a scale-free network configuration, and classical stochastic resonance curve showing the SNR and amplification factor versus noise strength in an uncoupled system. Selected publications
|

 POSTDOC position NOW OPEN!
POSTDOC position NOW OPEN!